Régularité des applications
La régularité d’une courbe encode à quel point il est facile de glisser son doigt sur celle-ci. Les courbes suivantes présentent différents niveaux de régularité.
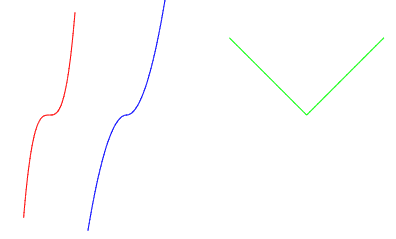
Définition
On définit la régularité d’une courbe comme le moment où un pic apparaît en prenant ses dérivées successives (ses droites tangentes).
La première courbe a régularité infinie, la seconde régularité 1 et la dernière régularité 0.
Des plongements étranges
La première et la seconde courbe semblent à première vue très similaires, pourtant elles diffèrent beaucoup.
Par exemple avec des applications du second type nous pouvons ranger un tore plat dans \( \mathbb{R}^3 \) ou bien ranger de manière isométrique la surface de notre plan`ete autour d’une balle de tennis... ce que nous ne pouvons pas faire avec des applications du premier type.
Une toute petite Terre

Source : E. Bartzos, V. Borrelli, R. Denis, F. Lazarus, D. Rohmer, B. Thibert — hevea-project.fr, CC BY-SA 2.0 FR
Vivre dans un espace singulier
En vivant sur un espace rangé de manière singulière, on ne ressent pas forcément cette singularité. Par exemple, en vivant petit sur le cube, nous ne ressentons pas le côté singulier des arêtes (on peut le déplier sans changer les distances).
Par contre, nous pouvons détecter l’existence des sommets sans les toucher…
La somme des angles d’un triangle
Sur le dessin suivant, la somme des angles du triangle vert est 180 degrés (c’est un espace plat), celle du triangle rouge est 270 degrés et celle du triangle jaune 90 degrés. Cette différence permet de détecter la forme de la singularité sans la toucher.
