Impossible dans le monde régulier
En mathématiques, il existe de nombreuses situations où construire un objet géométrique respectant certaines contraintes est impossible dans le monde lisse.
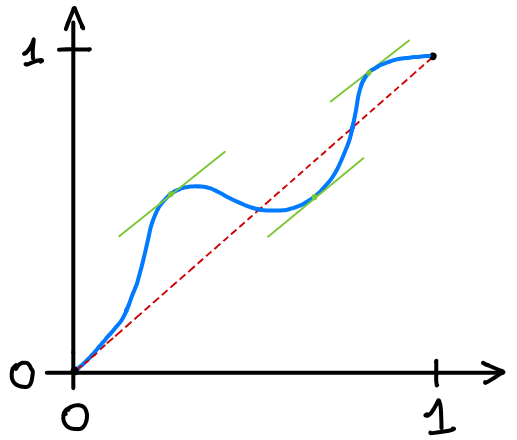
Par exemple, le théorème des valeurs intermédiaires dit qu'il est impossible de trouver une fonction \( f : [0,1] \to [0,1] \) partant de 0, arrivant à 1, avec un graphe « sans coins ni sauts » et « presque plat partout ». Il faut forcément qu'à certains endroits la pente soit 1 ; pas d’échappatoire !
Et avec singularités ?
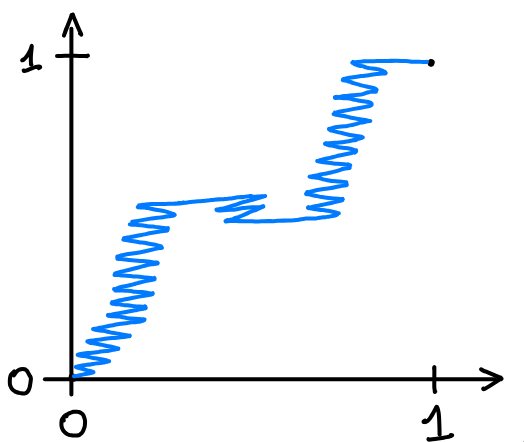
Mais que se passe-t-il si l'on autorise l’ajout de coins au graphe ?
En ajoutant de nombreux petits zig-zags, on peut aller de 0 à 1 tout en gardant la pente presque nulle partout, et en restant proche du graphe précédent !
Comment grimper une montagne trop raide ?
Cette « méthode du zig-zag » est utilisée dans la vie de tous les jours. Par exemple, imaginez que vous voulez construire une route pour monter une montagne très raide.
Si vous tracez une ligne droite du bas jusqu’au sommet, la pente est trop forte : impossible à gravir. Pour rendre la montée possible, il faut faire des virages en zig-zag, c’est-à-dire serpenter le long de la montagne.
Chaque virage rend la pente moins raide, et permet de progresser même si la montée serait trop difficile en ligne droite.
Des dessins aux h-principes
En mathématiques, la même idée se retrouve dans plusieurs contextes : certaines constructions d’objets géométriques sont impossibles si l’on exige qu’ils soient totalement lisses, mais si l’on accepte de petites « irrégularités » (des zig-zags ou singularités), alors on peut atteindre le résultat souhaité.
Les singularités ne sont donc pas forcément des « horreurs » à éviter, mais aussi un outil puissant pour réaliser l’impossible !
La question devient alors de comprendre quel est le type de singularité le plus simple qui permet d’achever la construction souhaitée.
Cette stratégie et cette question sont à la base d'une théorie mathématique qui s'appelle la théorie des h-principes, ou les principes d’homotopie.