1. Points critiques
Imaginez que vous êtes une fourmi qui se balade sur une surface (un ballon, une tasse...). Lors de cette promenade, vous allez gagner ou perdre en altitude. Certains points sont comme le sommet d’une colline et vous avez vue sur le paysage environnant. D’autres points sont des fonds de vallées, et les environs sont plus hauts que vous. Enfin, vous passerez des cols : dans une direction vous suivez la crête alors que dans l’autre vous descendez. Ces points sont les points critiques de l’altitude.
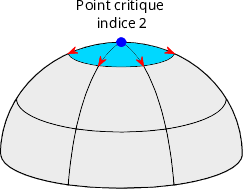
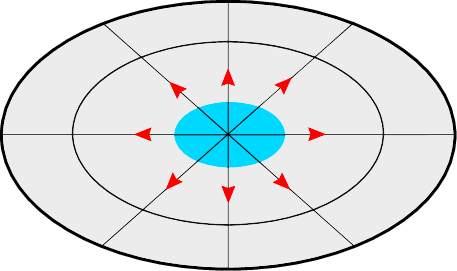
- Un sommet (resp. une cuvette) est localement un maximum (resp. minimum) de l’altitude. Une goutte d’eau s’y étale (resp. contracte) dans toutes les directions (voir 2).
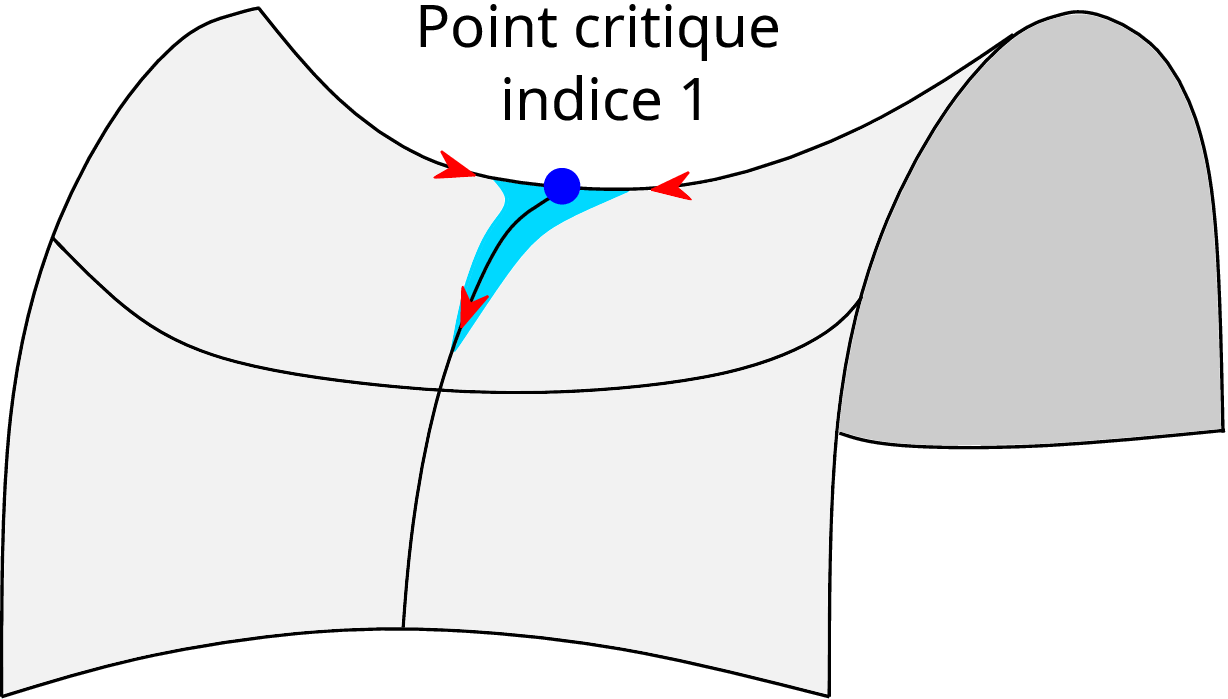
- À un point col, il y a deux directions privilégiées. Sur l’axe reliant les deux vallées, l’altitude est maximale tandis que sur l’axe reliant les sommets, on est à l’altitude minimale. Une goutte d’eau s’étale dans la première direction et se contracte dans la seconde.
2. Maximum
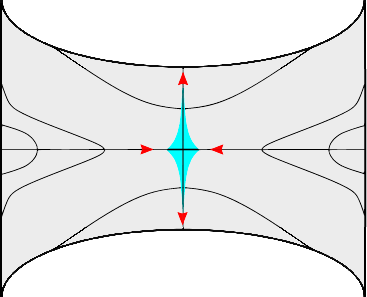
3. Point col
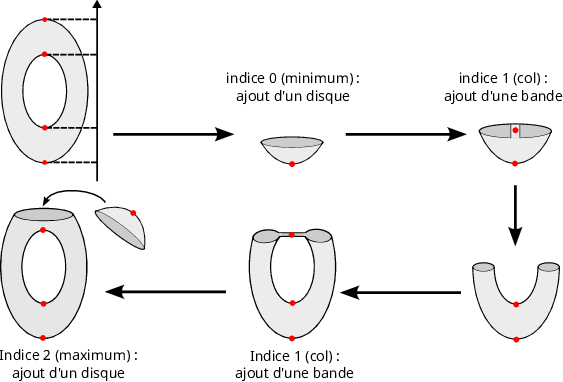
4. Comprendre la forme d’un tore à partir de ses points critiques
Etudier la forme d'une surface \(M\), c'est étudier cette surface à déformation continue près. Si on imagine jouer avec une boule de pâte à modeler, la forme de la surface de la boule reste la même quand vous étirer la pâte (déformation continue) mais change quand vous faites un trou (déformation non continue).
Un sous-niveau \(M_a\) d'une surface, correspond à tous les points de la surface situés en-dessous de l'altitude \(a\in\mathbb R\). De même une tranche \( M_{a\lt b} \) correspond aux points de la surface dont l'altitude est comprise entre \(a\) et \(b\in\mathbb R\).
Théorème
Si une tranche compacte \(M_{a\lt b} \) de surface ne contient aucun point critique, alors les sous-niveaux \(M_a\) et \(M_b\) ont la même forme.
On en déduit que si on regarde un tore en partant de l'altitude la plus basse et en montant petit à petit, la forme de la surface observée ne peut changer que lorsqu'on passe des points critiques. Plus précisément, on a :
Théorème
Passer un point critique d'indice 0 correspond à ajouter un disque, un point critique d'indice 1 à attacher une bande (aussi appelée anse, comme sur un panier) et un point critique d'indice 2 à recoller un disque le long de son bord.
Les théorèmes présentés ici sont des cas particuliers de résultats plus généraux. On peut remplacer "surface" (dimension 2) par "variété" (dimension n), la fonction altitude par n'importe quelle fonction \textit{lisse} dont les points critiques sont non-dégénérés.
5. Reconstruction du tore